
Fundamentals
How to Make Stuff Move
When programming virtual worlds, or anything 3D in XNA, you are going to have to describe, understand, and command movement.
I don’t know how much of this is obvious, and how much of it is learned. But, I wanted to talk about 3D space and kind of make sure that we all understand the basic concepts that everything in 3D programming is based on.
Who Can Skip This
If you understand the difference between a left handed coordinate system, and a right handed coordinate system, you know basically what causes Gimbal Lock, and just can’t stand to listen to me ramble aimlessly over the meaning of life, the universe, and everything, then you can skip this section. Incidentally, I won’t be discussing Gimbal Lock at all in this section or explaining the difference between a right and left handed coordinate system. I will however be rambling aimlessly over the meaning of life, the universe, and everything. Consider yourself fairly warned.
What You’ll Learn in this Section (Hopefully)
What dimensions are, which you will need to understand movement and vectors.
Dimensions
What’s the difference between 2D and 3D? Obviously, one more dimension. But have you ever stopped to think about what a dimension actually is?
I knew this guy in grade school that convinced me that he understood the “4th dimension”. (Hey, give me a break I was a young kid that didn’t understand what a charlatan is.) As an adult, I realize he was just doing what we call “blowing smoke”. But it brings up the point that the word dimension is often not understood, misunderstood, or only partially understood. And the word itself has a tendency to automatically make us think that we’re talking about something that is “unknowable”.
I looked up the word “dimension” at Merriam-Webster.com and was surprised to find out that they seem as confused about what a dimension is as everyone else. I think the definition that most closely fits the difference between 2D and 3D, as well as the definition that most closely matches the way I will be using the word, is “d: the range over which or the degree to which something extends”. That really describes a range and not a dimension. It definitely doesn’t tell you what the difference between a range and a dimension is. So, let me make up my own definition that I think will help you understand dimensions for the rest of your life:
Dimension – Two things that are one and the same, but naturally oppose one another.
Wow. That sounds as crazy as most of the other definitions of the word dimension. So, let me explain what I mean.
A dimension is something that has two directions that oppose each other. For example, up and down – as positions – are the same thing. The more you go up, the less you are down. And the more you get down, the more funky you are… sorry… I couldn’t resist. The more you go up, the less you are down, and the more you go down the less up you are. The two are really part of the same thing, but on opposite ends. Or if you want to sound really smart when you talk about it you could say “The two are opposite directions of a common continuum”. But who really wants to sound that smart?
Another example of a dimension is profit and loss. The more profit you make the less of a loss you have. The more of a loss you have the less profit you have.
Another example, the more fat you are, the less skinny you are. The more skinny you are, the less fat you are.
Another example, the hotter something is the less cold it is. The colder something is the less hot it is.
So, “basically” a dimension is something where you have two opposites that are part of the same thing. The fact that they have this relationship where becoming more of one automatically means less of the other is what makes them a dimension.
In math, we like to represent dimensions with positive (+) and negative (-). Which side gets to be positive and which side gets to be negative is really a matter of personal choice, or – more commonly – tradition. Zero indicates a balance between the two opposing sides. Anything that is positive represents an increase on the positive side and anything that is negative represents an increase on the negatives side. Since they are in a “tug of war” with each other, any increase of one decreases the other. For example, when you move to the left side you are increasing your distance towards the left but also decreasing your distance towards the right.
Positive and Negative is really where my definition came from. The question was “What does positive and negative mean in the real world?” The answer was “They are movements across a dimension”. And that lead me to my definition of a dimension which seems to hold true in pretty much all of mathematics even leading towards an understanding of things like “imaginary” numbers and the reason a square root has two answers where it should only have one. But I’m going off on a tangent now. Back to XNA.
3D space is 3D because it has 3 dimensions. Those dimensions are Forward-Backward, Left-Right, and Up-Down. You could also think of them as North-South, East-West, and Up-Down except that that has no meaning in outer space or any place where there is no North Pole (In reality, East-West happens on a sphere and is circular motion, which really makes it not the same thing at all, but whatever helps you envision the space is good by me.)
3D could also be represented with Fore-Aft, Port-Starboard, and Below-Above. This actually might be the best way to represent 3D, because up and down are due to gravity, but below and above are not. But, everyone pretty much universally thinks of 3D space as Forward-Back, Left-Right, and Up and Down. So, that’s what we’ll stick with.
Now, it’s one thing to imagine things moving around in 3D space, but the computer actually has to draw them. So, the computer really needs to describe things in 3D space using numbers. Mathematicians use a number line to describe positive and negative changes in one dimension. For 2D they like using an X,Y graph that you are hopefully familiar with.
In XNA we talk about positions in 3D space using x,y,z axes.
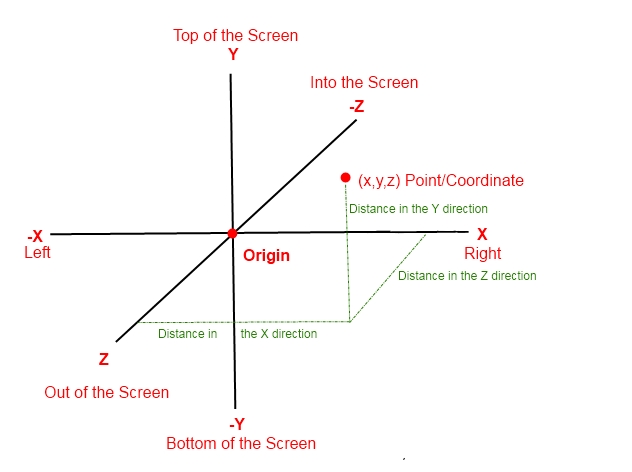
The X axis is the dimension of Left and Right. The Z axis is the dimension of Forward, or into the screen, and Backwards, or out of the screen. The Y axis is the dimension of Up, or towards the top of the screen, and Down, or towards the bottom of the screen. Notice that moving forward (into the screen) means becoming more negative. That may seem a bit odd, but that’s the way that XNA does it. So, you pretty much have to live with it.
In order to describe movement in this 3 dimensional space, we have to discuss it as movement away from one specific point. That point is called the origin.
The origin is the center of your 3D virtual world. It’s the point where X=0, Y=0, and Z=0. When any of those numbers change it will represent a distance away from the origin. So, a point in your 3D universe that is (3,2,4) is 3 units to the right, 2 units upwards, and 4 units back (as if coming out of the screen).
A couple of things you don’t want to get “caught up on” are units and camera facing. The first is units. The x,y,z distances could be measured in feet, inches, meters, kilometers, or parsecs. The represent whatever you want them to represent. You just have to make sure that, whatever you decide they represent, you stay consistent. Drawing one object and saying they represent inches and another while saying they represent meters is going to cause all your objects to be really odd sizes and distances from each other. Pick one type of unit and stick with it. Meters is probably the most common, but there’s nothing wrong with making them equal feet. Just be aware that all the units in your physics formulas have to basically be the same too and physics likes the metric system. You’ll probably see me using meters, and the metric system, most of the time even though I’m American. A meter is roughly the length of a yard. So 100 meters is roughly the size of a football field. Yes. I said it. Football. Not soccer. Incidentally, why do we call it football? Other than the occasional punt you don’t even touch it with your foot.
The second “hang up” point is camera facing. I describe x,y,z in terms that assume we are standing at a specific point. The problem is that you can, and will, move the camera, that you will view this word through. So, if we flip the camera around to the other side, negative Z will be coming out of the screen and positive Z will be going into the screen. Most of the time, you’re probably going to be thinking of x,y,z as if the camera was permanently fixed to a spot that is somewhere out in the positive z area.
Movement in 3D space is just a matter of increasing the numbers in the position. So, if the position is 4,2,7 then increasing it to 6,2,7 causes it to move 2 units to the left. Incidentally, this coordinate system uses floats, or real numbers with decimal places, so you can move to 6.333,2.1,7.891303 if you like.
For a lot of things we will load up a matrix with the movement and then “apply it” but that’s another subject.
The Bottom Line
You have to have some understanding of the x,y,z axes and what it means to move along the dimension of each axis (between negative and positive). You also need to know that the center of the 3D world (the origin) is at x=0,y=0,z=0.