
What's Your Vector Victor?
Vectors are so common in game programming that I really need to take the time to help people try and grasp the subject. Vectors are unbelievably easy to understand other than the fact that you need trigonometry to rotate them and they do this thing called “multiplying vectors” which isn’t really multiplication. I can understand why that confuses people. But, vectors themselves are really easy and the other problems such as the trig and multiplication can be overcome.
I think vectors are one of those things that are incredibly difficult until you have that epiphany, or “Ah HA!” moment, where you just “get it”. Then from that point on it’s just obvious. And I think the key to reaching that point is understanding what a vector is and not trying to make it into something that it’s not.
So what is a vector anyway? A vector is nothing more than an amount that is permanently tied to a direction. That’s it. Period. Great we can all go home now... Except that, for whatever reason, this seems to be a really difficult concept for almost everyone I’ve ever met.
In my trigonometry class, about 75% of the people dropped the class before we got to Vectors and the people that were left just understood them well enough to pass the test. I could even tell that the guy teaching the class had no idea what they are but was simply teaching them straight out of the book.
So, maybe the best thing to do is start out by
talking about what vectors are in the real world and how they apply to
the real world.
Why We Need Vectors (or Everybody do the Robot!)
Ok. Let’s say we’ve got this remote controlled robot out in the front yard that we can remotely tell it to move and pick stuff up. We move it by giving it instructions. We’re up on the balcony controlling it remotely and can’t touch it or move it ourselves. All we can do is tell it to move.
So, let’s say we want our robot to move to a spot
and pick up an apple. It has to move to the apple in order to be able to
pick it up. The apple’s position relative to the robot is 4 meters to
the right and 7 meters forward.
So you tell the robot “move 4 meters”. And the robot moves 4 meters to the left. Wait! That’s making it worse! That’s not what we wanted. But the robot obeyed. It did exactly what we told it to. Now we need to move it 8 meters to the right. So you tell the robot “move 8 meters” and being the smart alek robot that it is it moves back and forth for a total of 8 meters dancing about and coming to rest in the exact same spot it was in before.
The point to understand here is just supplying an amount is not enough to get the job done.
So now you tell the robot, “Move RIGHT!” because by this time you’re obviously yelling, right? The robot proceeds to obey the command exactly as given and moves 10 meters to the right. Now, it’s gone too far to the right.
The point to understand here is that just supplying a direction cannot get the job done.
So, quite obviously you need to tell the robot a direction and an amount. So, you’ve got a handy reset button that tells the robot to go back to its starting position and once again the apple is 4 meters to the right and 7 meters forward. So you tell the robot “Move 4 meters forward”. “Now move 7 meters right”. Except, wait. That’s not right. The robot does exactly what you said and yet it doesn’t move to the apple. Instead it moves to a new position where the apple is now 3 meters to the left of the robot and still 3 meters forward.
But it did exactly what you told it to. You say, well, I didn’t mean “Move 4 forward and 7 right. I meant 7 forward and 4 right.” But you gave the correct directions and you gave the correct distances. The problem is that we didn’t attach the correct distances together with the correct directions.
The point here is that, in order to give the correct orders, the correct directions have to stay attached to the correct amounts. Just because you have the correct amounts, and just because you have the correct directions is not enough.
That is what a vector is in the real world. A direction for this problem is meaningless by itself. A distance by itself is meaningless. The only thing that can solve the problem is a vector because a vector has amounts and direction tied together permanently. Moving 4 meters to the right is totally different from moving 4 meters up. And moving 5 meters forward is totally different from moving 7 meters forward. The direction and the amount have to be treated as one thing.
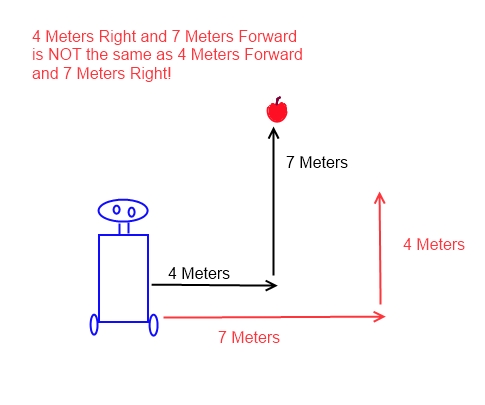
We usually imagine vectors as being arrows. So, in our robot problem, we could give it a vector of “4 Right” and then “7 Forward” and send it straight to the apple.
Notice that we represented vectors as arrows in the drawing above and that adding the first vector to the second one combined them to give us our new position. Theoretically, we could have had one vector that just told the robot “Turn to an angle that faces the apple and then go this distance”. We would have to do some trig to get the angle, and we would have to use the Pythagorean theorem to get the length, but we could combine those two vectors together into one vector. Either way, the end result is ending up at the apple.
And notice that vectors don’t have position. Or rather, their position is completely relative. In the real world we don’t have an X,Y =0,0 spot. There is no center of the universe and if there were it definitely wouldn’t be in my front yard. I said the robot started in the center of the front yard and maybe that’s confusing. But what if I start the robot at my front door? That’s not a center, or an origin, or a X,Y=0,0 spot. It’s just my front door. If I tell the robot move “4 Right” and then “7 Forward” it’s from my front door and not a X,Y = 0,0 spot. I’m just saying “move that much from wherever you are at currently”. I don’t care really where it’s currently at, I just want it to move that much.
So, keep in mind that vectors don’t necessarily have a position. You will mostly apply them to a position. In other words, “I don’t care what your position currently is Mr. Robot. Move 4 Right, and then 7 Forward from WHEREEVER you are at now and that new spot is the position I want you to end up in.”
So, it’s real important to see that most of the time the position of the vector doesn’t matter. That’s going to be real important as you start to think of vectors as arrows because you don’t want to get too hung up on the position of the arrow.
Vectors fill this very specific need in the world of describing things where the amount and the direction cannot be separated from one another. The reason the amount can’t be separated from the direction is that separating them may result in the wrong answer. If they get mixed up, it will definitely result in the wrong answer.
It’s kind of difficult to see why you need vectors when our directions are right-left and forwards-backwards. That’s not really the way vectors are used. The reason is is because the robot can move in other directions besides just right-left and forward-back. The robot could move 4 meters 48 degrees from due north. We still have a direction (48 degrees from due north) and an amount (4 meters), but now you can see that it’s not quite so easy to determine exactly where that vector points to.
When you actually get to using vectors they are going to be pointing in weird directions all the time. So, it starts making even more sense to treat them as vectors when they do that.
I mean, what if the correct directions to the apple were “4 meters at 84 degrees from due North and then move 7 meters at 14 degrees from due North”. Maybe there are a lot of rocks in the yard that make only that one path traversable for the robot. That’s when using vectors really starts making sense.
Simple movements left-right and forward-backwards may be easier to handle without using vector math.
But in XNA we’re going to use vectors for just about everything.
Combining Vectors (aka Vector Addition)
Now you may have realized that there’s an easier way. I mean, why can’t you just tell the robot to go straight to the apple. Why do we need two vectors? Why can’t we just combine them into one vector and use that vector? Well, we can.
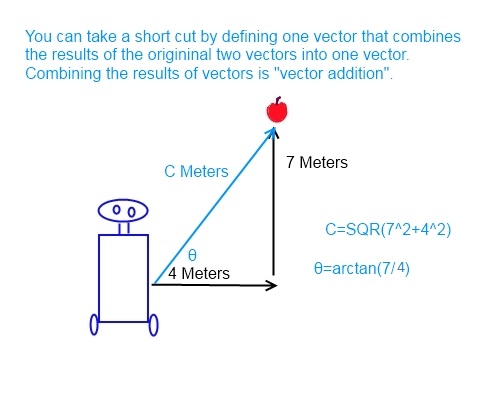
Adding 4 Right to 7 Forward results in a vector that goes straight at the apple. Unfortunately, we have to use trigonometry to find that vector unless we do it the way XNA does it. We’ll look at the way XNA does it here later.
The length of the combined vector is the Pythagorean theorem because this happens to form a right triangle. The Pythagorean theorem says that the hypotenuse of a triangle, represented by C, equals the square root of the combined square of both sides or C^2=A^2+B^2. That will give you the new amount which is also the distance to travel in the direct route.
Before we had due right and straight forward. Since we’re going at an angle, we don’t have that convenience and we start really seeing why vectors are important. To calculate the angle, you pretty much have no choice but to use trigonometry to find the angle as the arctangent of 7 divided by 4. If you haven’t taken a trigonometry class, don’t get too intimidated by that. Even those of us who are very experienced calculating arctangent or tangent use a calculator. If you can hit 7 divided by 4 and then the arctangent button you can probably get the angle in radians (Radians are a measure of angles like degrees. You may be able to figure out how to make the calculator give you answers in degrees rather than radians until you learn to use radians).
The point is that you can add vectors together and get one vector that represents the vectors that you combined by adding them together. Adding vectors just combines them into a single vector.
Notice that when we place the tail of the 7 meter vector to the head of the 4 meter vector they start at the same place as the combined vector and end at the same point as the combined vector.
In math class they will probably let you do vector addition this way by putting them head to tail. But keep in mind that it didn’t matter the position of any of these vectors. They only represent amount of movement and directions of movement. The starting point is unimportant. And the ending point is always going to be the starting point plus the vectors, equaling the ending point, no matter what the starting point or ending point is.
Representing Vectors
You can represent vectors in several different ways. It doesn’t matter how you represent them as long as you understand what they are in the real world. We pretty much always use arrows to represent vectors because they do a good job of showing us that the vector represents an amount and a direction together. Other than that, you will see vectors represented several different ways in the math world.
So, let’s start with “2 coordinate vectors”.

A Vector is an amount tied to a direction. So we represent a 2D vector using an arrow. In math class they often represent the vector with two points on an X,Y axis graph. One point is the tail of the vector and the other point is the head. The direction of the vector is whatever direction is pointed at as you move from the tail point to the head point. The amount of the vector is its length from tail to head. The length of the vector is also sometimes called its magnitude.
Vectors in XNA
XNA does not represent vectors this way, and usually neither do experienced mathematicians. The reason is that only the amount and direction of the vector is important. So we don’t really care where the tail is at or where the head as at as long as the vector maintains the same length and the same direction. Position just simply doesn’t matter. (And that goes back to the mantra “A vector is nothing more than an amount permanently tied to a direction.")
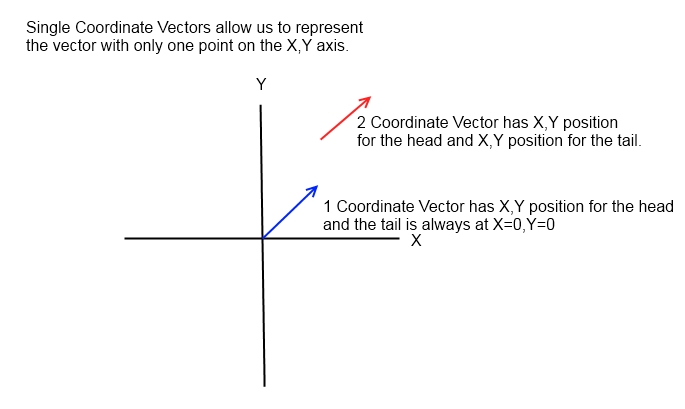
So, in XNA we just have a standing rule that the tail is always at X=0, Y=0 (or for 3D X=0,Y=0, Z=0). One of the advantages that gives us is that we only have to keep track of one point (the head) instead of two points.
We can represent 4 units right with a vector of X=4, Y=0. And we can represent a Vector of 7 up or forward with X=0, Y=7. And adding the two vectors together gives us a tail that’s still at 0,0 but now the head would be X=4, Y=7. That’s the combined value of the two original vectors.
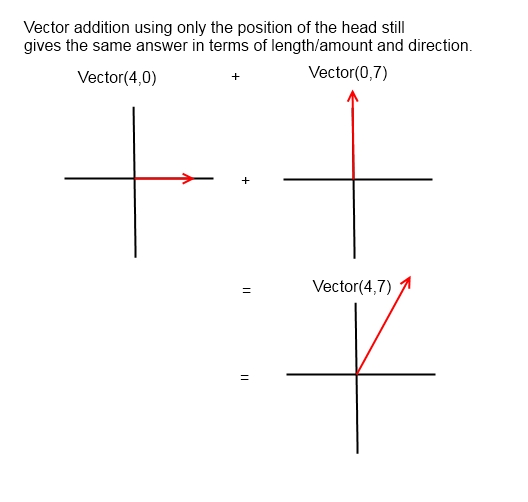
Notice that we are representing the answer/result vector without resulting to calculating an angle or working through the Pythagorean theorem. The answer vector is just 4,7. We can calculate an angle for that vector - if we really need to - but a lot of times we don’t really need to. We just know that whatever angle that is, it’s the angle that we need to travel at, and we won’t worry about it until the moment when we need to know what the actual angle is. Then we can calculate it using the same arctangent formula previously mentioned or possibly by some other method.
Positions are NOT Vectors
One of the places where people often get confused is that XNA uses Vectors to store positions/coordinates/vertices all the time. These are not really vectors. They store very nicely into XNA Vector objects because Vector objects in XNA are just the coordinate of the vector’s head. But that doesn’t make them vectors just because they store nicely in a vector object.
If you want to get really technical, you can say “Well, a position is a vector because the amount is the displacement from the origin (0,0) and the direction is the direction from the origin to the point.” Technically, that makes it a vector. And the plus side is that that allows you to use points in vector math as if they were actual vectors. But honestly no one cares about the displacement or a point, or coordinate, from 0,0 or the point's direction from 0,0 to the point outside of forcing it to be a vector for the math. So, it’s not really a vector. Just don’t let it confuse you.
Thinking of a position as a vector is really helpful though when adding it to vectors. When the position is a vector you can just add the position vector to the actual vectors to get a new position vector as the answer. So, in that sense it’s ok to think of a position/coordinate/vertex as a vector. Just don't let it confuse you!
Vector Movement
Most of the time you will add vectors in XNA. More than anything, you will store positions for things as vectors. Then you will add some sort of movement vector, or combination of movement vectors, to that position vector in order to find a new position vector(point) that is the end result of all the movement.
This allows you to move at odd angles. I mean, without vectors it's tempting to just move things by adding or subtracting values to X, Y, or Z (in 3D). That tends to lead you to moving with integer values. I mean think about it for a minute. Doing it like that are you going to say move 3 units along X and then 4 units along Y, or are you going to say move 4.3 units along X and 2.1154 units along Y at the same time because I want you to move at that angle. Do you even know what that angle is?
But if you load a position into a vector that represents the position of the object. Then you create a known vector such as Vector3.Forward that has a known value of (0.0,0.0,-1.0) or one unit down the Z axis in 3D. Then you create a rotation matrix with a rotation amount and rotate that known vector by a given angle in the rotation matrix. This gives you a vector that points to a known direction (angle) in 3D space. At this point you have no idea what is in X,Y, or Z, but you know that it points at the exact direction that you want.
So, vectors are really good at keeping track of things like what direction an object is facing (especially in 2D because it's a bit more complicated than that in 3D). And they're really good for saying, move 3.7 units in the direction that is 42.7 degrees to the left of what direction you are currently pointing to.
You can make a game where the player and the objects can only face directly north, south, east, or west. But if you want them to face any direction in a 360 degree circle, that's where vectors really start coming in handy.
How to do Vector Movement
So, to do vector movement in 2D XNA, you want to store the position of the object as a Vector2. You want to treat the Vector2 position as an object rather than treating it's X and Y parts as much as possible.
When you want to move that object, you create another Vector2 (2D vector) with a known direction. Then you can use the rotation formula to rotate the vector to whatever angle you want the movement to happen at.
x = X * (float)Math.Cos(TurnAngle) - Y * (float)Math.Sin(TurnAngle);
y = X * (float)Math.Sin(TurnAngle) + Y * (float)Math.Cos(TurnAngle);
So, now this second vector has the direction that you want the movement to happen in and a length of one. (Normalize the vector if it doesn't already have a length of one.) Then you can multiply the second vector by the amount of movement you want to change it's length to that amount. And finally you add the new movement vector to the position vector. Note that you do not add their X and Y coordinates (which will work) but add the entire position vector to the entire movement vector. This is vector addition, not coordinate addition. It's just pointless extra work to have XNA add all the coordinates together when you can instead just add the vectors to one another directly.
Vector Normalization
The length of a vector is extremely important most of the time because a vector is an amount, or length, permanently tied to a direction. But sometimes you just want a vector to represent a direction. For example, in 2D you may want to keep track of what direction an object is facing on a 360 degree facing. You could keep track of that as an angle. But using vectors is often easier and maybe more accurate.
In order to use a vector as a direction without an amount, you want to basically cancel out the amount.
If you sent a vector's length to zero then the arrow has a length of zero and it ceases to exist. If it has no length then it can't have a direction.
So, instead we set the length to one. That's what we call a "normalized", or unit, vector. A vector is normalized when it has a length of one.
Normalized vectors are so common in 3D programming that they have a nickname. A normalized vector is called a "Normal". Also, don't forget that it may be called a "unit vector".i
This follows the normal laws of math where one times anything is going to equal that other value. For example,
1 * 23 = 23.
32.71652 * 1 = 32.71652.
Anything * 1 = that same Anything.
So following that idea, a vector with a length of one times any value will give you a vector, as the result, that has the length of that value.
Unit, or normalized, vectors are very useful for storing directions that have no specific amount. They are also good for setting the amount of a vector without changing it's direction.
Controlling a Vector's Length
The length of a vector represents it's amount. That's a very important part of what a vector is. So, being able to control that amount is very important also.
XNA has a Length() method to get the length of a vector. (A vector's length is also known as it's magnitude). So, you really don't need to know the math to do it.
To set the length of a vector, all you have to do is normalize it (set it's length equal to one) and then multiply the vector object by the length that you want.
XNA has a method for normalizing vectors. So again, you don't need to know how to do that.
Once it's normalized (has a length of one) than any number you multiply it with will be it's new length. In code it looks like this:
Vector3 MyVector;
MyVector = new Vector3(3.0,4.5,-1.7); //Use any vector.
MyVector = MyVector.Normalize();
MyVector = MyVector * 8.27;
In the example above, MyVector now has a length of 8.27 regardless of what direction it points in or what it's length was before. It will continue to point in the exact same direction as before, but it will just now have a new length.
This works exactly the same with 2D vectors as it does with 3D vectors. The end result is a new vector with the exact same direction but a length that you specify.
Notice that we took a vector object and multiplied it by a number! That's important to see. We didn't multiply the X,Y, and Z values by a number (although that's basically what XNA does in the background for this). Instead we just multiply the whole object times a number and XNA knows how to carry that out.
Incidentally, multiplying a vector times a regular number is called multiplying a vector times a scalar. Regular numbers are "scalars" which highlights the fact that they are not vectors.
Vector Addition
We've already kind of discussed vector addition. Basically, vector addition is like putting the tail of one vector up against the head of another vector and then creating a new vector that has a tail at the first vector's tail and a head at the second vector's head.
In other words, it creates a new vector that points to the spot where the two vectors combined point to but instead uses a single vector.
Or, you could say, adding vectors combines them into a single vector that starts at the same starting place and ends at the same ending place, but just goes in a straight line to get there.
In code it looks something like this:
Vector3 MyPositionVector;
Vector3 MyMovementVector;
Vector3 MyEndingPostion;
MyPosition = new Vector3(0.02,-3.4,-2.6);
MyMovement = new Vector(0.03,2.7,8.13);
MyEndingPosition = MyPostion + MyMovement;
Notice that I didn't mess with the X, Y, and Z values of these 3D vectors other than initially creating the vectors. Normally, you just want to set an X, Y, and Z starting position for their head and then not look at X, Y, or Z again after that. You just use the whole vector after that.
I don't really care where MyEndingPosition is at. I'm just going to tell XNA to use that position vector to draw my object, but it's exact X,Y, and Z coordinates don't matter. In fact, once these coordinates can get so complicated so quick that there's no way they can have any meaning to you. Once you rotate them in 3D a few times, change the vector's length, and add it to a couple more vectors the X,Y,Z coordinates of the vector's head are going to be something like (-82.187464646,132.0000032374,-26.05050583634). Seriously. Can you tell me what exact angle that is off the top of your head? Can you even tell me what vague direction that points in without a whole lot of thought? Can you tell me it's length without calculating it?
So, you mostly forget about the X,Y, and Z coordinates of a vector once you finish creating it.
Using Vectors to Keep Track of Facing
One of the main uses for vectors is to keep track of which way an object faces. This is especially useful in 2D. In 3D, the vector by itself does not know which way is "up", so a vector by itself is not enough information to know whether the object is upside down or not. Especially, in 3D you will often use a matrix to keep track of which direction an object is facing.
But especially in 2D you can use a vector that has been normalized (set to a length of one) to represent a direction such as the direction an object faces.
Theoretically anyway, rotating a vector should not change a vector's length. So there may be no need to re-normalize it. However, rounding errors are possible. So keep that in mind.
When you have an object's facing stored as a vector, you can do code like this:
Vector2 ObjectsPosition;
Vector2 ObjectsFacing;
float HeadingChange;
float DistanceToMove;
HeadingChange = MathHelper.ToRadians(22.6433);
DistanceToMove = 0.00243;
ObjectsPosition = new Vector2(-3.0, -12.21); //Set this once and forget about it.
ObjectsFacing = new Vector2(0f,1f); //Starting facing, but changes.
ObjectsFacing.X = ObjectsPosition.X*(float)Math.Cos(HeadingChange) - ObjectsPosition.Y * (float)Math.Sin(HeadingChange);
ObjectsFacing.Y = ObjectsPosition.X*(float)Math.Sin(HeadingChange) + ObjectsPosition.Y * (float)Math.Cos(HeadingChange);
ObjectsPosition = ObjectsPosition + (ObjectsFacing * DistanceToMove);
This is really good for getting away from moving at perfect 45 or 90 degree angles that you are inclined to move in without vectors in 2D.
You can do basically the same thing in 3D, but you have to remember that a 3D vector by itself can't keep track of what direction is "up".
Another difference is that you use matrices for the rotation rather than the rotation formulas. (The matrices actually use the rotation formulas internally, but it's easier and better to use the matrices. One reason it's better is that you can store more than just rotations in the matrices, plus the ability to combine multiple rotations in a matrix).
The fact that you can't keep track of "up" with a single vector in 3D "may" not be a problem depending on your program. For example, if you have a car that just moves along the ground you really are not moving in full 3D but instead moving on the 2D plane of X,Z in a 3D world. In that case you can use a Vector2 to represent the facing of the car. Now you may want the car to jump in the air and roll in a crash and then you may have to abandon this treatment.
Typically people and characters are rooted to the ground in a 3D environment. Even when they can jump or climb stairs they often are always in a heads up position. It's unusual to see a character standing on his head in a 3D game. It's possible, but not exactly normal. So it may make sense to treat the facing direction of characters as a Vector2 even in 3D environment and just represent their altitude as a separate number. Then the position movement of a character might be something like:
Vector3 CharactersPosition = new Vector3(2.0,0.0,-4.2); //Y stays at zero.
Vector3 CharactersFacing = new Vector3.Forward;
float HeadingChange = MathHelper.ToRadians(8.2); //8.2 degrees
float DistanceToMove =4.6;
Matrix Rotation = Matrix.Identity;
Rotation = Matrix.CreateRotationY(HeadingChange);
CharactersFacing = Vector3.Transform(CharactersFacing, Rotation);
CharactersPosition = CharactersPostion + (CharactersFacing * DistanceToMove);
Again, we don't really mess with X, Y, and Z. Except that Y stays at zero. You might set Y as separate altitude value if the character were jumping or climbing stairs or something.
You could also do these as 2D vectors like in the first example and then just use the altitude as a Y value for positions and whatnot as needed.
Vector Negation
Vector negation means multiplying a vector by negative one. Multiplying a vector by the scalar value of one does nothing to change the vector. It's like multiplying any number times one; it doesn't change it. The negative, however, causes the direction of the vector to reverse direction 180 degrees. In other words, it causes the vector to turn and face the exact opposite direction without changing the length, or amount, of the vector.
This is exactly the same in 3D as it is in 2D.
Vector Subtraction
Vector subtraction is not nearly as common as vector addition. But it works basically the same way that addition and subtraction work with normal numbers. That is, it's the exact opposite of addition.
Vector subtraction does the addition process in reverse. If you have a result vector, and you subtract one of the vectors that you added, it will give you the other vector that you added.
Vector Rotation
XNA has some nice matrices for rotation in 3D. Unfortunately, I can't find any such thing in 2D. That means that you have to use the rotation formulas:
x = X * (float)Math.Cos(TurnAngle) - Y * (float)Math.Sin(TurnAngle);
y = X * (float)Math.Sin(TurnAngle) + Y * (float)Math.Cos(TurnAngle);
Notice that there's one formula for the X component and another for the Y component. That's just the nature of how the math works. I mean, really, you can only get one answer at a time when rotating a 2D point like this. There is no one number that represents an X,Y position. It's two numbers and so it requires two formulas.
And understanding how these formulas work is really ugly too. I couldn't hardly sleep until I figured out how these formulas actually worked. It took about a week and I ended up finding the formulas in the back of one of my trig books. It took pretty much every single concept in the trig book to understand, or prove, how these formulas work. I actually did prove the logic behind the formulas though. Now I can't remember the proof if my life depended on it, years later. Lesson learned = don't worry about it. It works. Just use it.
In 3D the formulas are exactly the same. In fact, they are so much exactly the same that all you do is apply the exact same formulas to the X and Y axes (the formula written rotates around the Z axis). This ultimately means that there is no such thing as 3D rotation using these formulas or matrices. All 3D rotation is done by rotating around a combination of the three axes one at a time. Quaternions can handle it in one rotation, but that's another subject.
To rotate in 3D you use these matrices:
Matrix.CreateRotationX (Single)
Matrix.CreateRotationY (Single)
Matrix.CreateRotationZ (Single)
This example rotates a 3D vector around the Y axis
Vector3 CharactersPosition = new Vector3(2.0,0.0,-4.2); //Y stays at zero.
Vector3 CharactersFacing = new Vector3.Forward;
float HeadingChange = MathHelper.ToRadians(8.2); //8.2 degrees
float DistanceToMove =4.6;
Matrix Rotation = Matrix.Identity;
Rotation = Matrix.CreateRotationY(HeadingChange);
CharactersFacing = Vector3.Transform(CharactersFacing, Rotation);
CharactersPosition = CharactersPostion + (CharactersFacing * DistanceToMove);
To combine rotations around different axes, you multiply their matrices together.
Differences Between 2D Vectors and 3D Vectors in XNA
In Xna, 2D vectors and 3D vectors are not all that different except for the obvious difference of a third dimension.
That third dimension is Z in 3D. Well, sort of. 2D can represent either a horizontal or vertical plane. If it represents a vertical plane that would be X,Y, but if it represents a vertical plane that would really be X,Z even though most people are still going to call it X,Y.
Vector addition and subtraction work the same way in 3D that they do in 2D except now you can have the head of the vector in all 3 dimensions (X,Y,Z).
This is really where vectors really start making a whole lot of sense to use. It's one thing to look at X,Y coordinates and know what they are. It's one thing to work with X,Y coordinates individually. But it's just a whole lot more complicated to work with X,Y, and Z. Working with vectors can make that a lot more simple.
Vector normalization works the same in 3D as it does in 2D, where it sets the length of the vector to one.
Negation still flips a 3D vector around like it does a 2D vector.
One thing you've got to watch out for in 3D is that a vector, by itself, doesn't keep track of which direction is up. So, if I have a vector that's facing a certain 3D dimension, I don't know how the object is rotated around that facing vector. A lot of times that doesn't really matter. For example, I don't need to know whether the gun is upside down or not to know that the barrel points in a certain direction and that the bullet will travel out from that direction and forward in that direction. So, a 3D vector is perfect for this.
But if you have a flight simulator where the plane can roll upside down, then simply knowing what direction the plane is facing (even in 3D is still not enough to know whether the plane is on it's side, upside down, or right-side up). For this sort of thing you should be thinking about matrices and quaternions.
Multiplying a vector times a scalar works exactly the same in 3D as it does in 2D, where multiplying the vector times a scalar multiplies it's length times the scalar value. This can be used to set the length by first normalizing the vector to one and then multiplying by the length you want.
Vector Multiplication (or Going Off the Deep End...)
We've already looked at multiplying a vector times a scalar (normal number). But what if you multiplied a vector times a vector. What would that even mean!?!?
We add and subtract vectors to vectors, why can't we multiply vectors to vectors? Well, the answer is because it doesn't really mean anything to multiply the combination of an amount tied to a direction to another amount tied to a direction. In the real world it's kind of a stretch to say that that has meaning.
However, when you go through all the steps of doing it, you find that there are two ways of doing it that end up producing some very useful results. The two "multiplication" methods for vectors are called the Vector Dot Product and the Vector Cross Product.
The Vector Dot Product
The vector dot product is usually done with two 2D vectors. I hadn't even really considered doing it with 3D vectors until recently. Even in a 3D environment you are usually treating the 3D vectors as if they are 2D when doing a dot product.
I'm not going to go into the math of how to compute a vector dot product. In fact, you may have noticed I haven't gone into much math on the entire subject of vector math. That's because XNA handles all of this stuff for you. If you need to, you can look up the formulas and copy and paste them, but you may never need to in XNA.
What you really need to know is what the Vector Dot Product is actually useful for. The answer is this:
The Vector Dot Product of two vectors casts a "shadow" of the first vector onto the second vector.
That may sound like me speaking in riddles again, but that's basically the way you need to think of it to make it useful. Technically, the Vector Dot Product gives a new vector that has the direction of the second vector, but a length that is the same as if the first vector had of cast a shadow of the first vector at a perpendicular angle to the second vector. That sounds more complicated to me then just saying "it causes one vector to cast a shadow on the other".
This is really useful for removing a dimension. Technically, the way that the dot product math is typically written you are reducing a 2D vector's head position down to a 1D number (length along the second vector). So, you're reducing 2D down to 1D.
Where you mostly see it used is when you want to reduce 3D down to 2D. In fact, it's a key part of turning the 3D world into XNA into a 2D image that gets drawn on the screen.
You'll also see it used in tricks such as the OBB(Oriented Bounding Box) used in collisions.
And the Dot Product is also good for several tricks in determining angles between two vectors, such as whether they are perpendicular or not.
When ever you see it used, you should think "Ok. The first vector is casting a shadow on the second vector to give me a new vector that has the length of the shadow, but the direction of the second vector."
You can use vectors quite a lot for a lot of things and never need to know this. But it is very handy for certain things.
Both Vector2 and Vector3 have a method for determining the Dot Product of two vectors. I think they are basically the same thing, but we only covered 2D vectors in my trig class in college.
If you want to know more about the Vector Dot Product, you can start with Wikipedia.
Vector Cross Product
Again, multiplying vectors against vectors is kind of one of those things where it's like "What does that even mean!?!?" But there are two ways to do it, not counting multiplying against a scalar.
The second method is the Vector Cross Product. The Vector Cross Product is used to add an extra dimension. Most of the time you will see it used to move from a 2D plane into 3D space.
The Vector Cross Product takes two 3D vector that represent a plane, and gives a third vector that points perpendicular perfectly out of that plane. In other words, it gives you the direction that the plane "faces".
You see this all the time in XNA 3D. The way that it is used is to get what they call a "Normal". Now, we've already said that a vector "Normal" is just a normalized vector with a length of one. That's true. That's ultimately why this is called a normal. We also said that a normalized vector represents a direction without an amount. Again, we are concerned about what direction faces away from the plane; so a normalized vector is what we want.
But most of the time, when you hear about normals in 3D they mean that they produced a normalized vector using the Vector Cross Product and then maybe changed it's direction as needed (it may no longer point straight out of the plane depending on how it's used).
You see this mostly in lighting calculations, but it's also common for terrain collision and such.
When you're thinking about the Vector Cross Product, you want to be thinking about the plane produced by two 3D vectors. If you think about it, that's exactly what a triangle, or polygon, is in XNA; two of it's edges can be turned mathematically into vectors. Then you can find the Cross Product and that will give you a normalized vector that points directly out from the polygon. You could use that vector to know whether the polygon is facing towards or away from the light source and how much light needs to be applied to it based on how it's angled into the light, for example. You might not light the back side at all.
One of the key things to notice there is that you have two 3D vectors that may not even be aligned with any axis. But they still represent a plane through 3D space (also not aligned with any axis) that both of the vectors exist on. The Cross Product gives you the facing direction of that 2D plane in 3D space. So, it's kind of like moving out of 2D into 3D. It's like a sign post that says "This way into the third dimension!"
Again, this is one of those that you may not use as often as vector addition. But it's something you eventually need to know.
It's also important to know that the order that you put the vectors in, when doing the Cross Product, will determine whether the result vector is pointing in or out from the plane.
The Vector3 class has a method for determining the Cross Product of two vectors. There is no equivalent method in 2D, which makes sense since the answer is really in 3D and so you kind of have to have a 3D environment for the whole thing to have meaning. But remember it's about finding the facing of a 2D plane in 3D.
Wikipedia is a place to start with finding more information on Vector Cross Products.
And That's It!!!
Believe it or not, that's basically all there is to vectors in XNA. If you've understood everything I've talked about here, you pretty much know everything you will ever need to know about Vectors for XNA or 3D game programming.
Summary
Vectors are used all the time in XNA and understanding them is fundamental to working with XNA.