
Acceleration of 2D Objects
May the Force be with you
This tutorial is going to teach you how to apply accelerations to objects. Notice that I keep using the word "acceleration" and not "force". "Acceleration" has a very specific meaning in the world of physics that actually has a relationship to "force" which is different.
You can think of an acceleration as a "push". If you momentarily shove an object, that would be an acceleration.
In the world of physics, an acceleration is defined as a "Force per Mass" or "Force/Mass". In more plain English, the "force" is really the force you apply in the shove. The mass is the mass of the object. You can think of mass as "weight" although "weight" is actually different. "Weight" is what happens to mass in a gravitational field.
If you went into space, you would become weightless, but your mass would remain the same. Mass is kind of like the weight of something even when its weightless.
So, it's really a force that pushes the object. And the more mass the object has, the less acceleration it causes. So, acceleration is basically the result of the force's push based on the mass of the object being pushed. Notice that we basically have the concept of momentum here; the more massive the object, the harder it is to accelerate it. You should also note that we will accelerate in the opposite direction to decelerate an object. So, even slowing down is an "acceleration". It's just an acceleration applied in the opposite direction.
It's probably a good idea to think of a force as a vector. A vector is just a direction permanently tied to an amount. The amount of acceleration produced by the force is important because the object's velocity, or speed, will be changed by the amount of the acceleration. But you can't ignore the direction that the force, or acceleration, was applied in. Pushing north is not the same thing as pushing an object south. In fact, they are exact opposites. So, if you apply a force northward and apply a force southward, the result will be that the two cancel one another out because they are applied in exactly opposite directions. That's largely why we use vectors for this.
A vector, again, is a direction tied to an amount. We generally think of vectors as arrows. In XNA, vectors are stored as positions. In XNA, a vector object holds the position of the vector's head. In XNA, the vector's tail is always at X=0,Y=0. Since that is the case, you can represent the arrow with only the position of the head to represent the arrow. The direction of the vector/arrow is from the tail at 0,0 to the position of the head and for an acceleration vector that represents the direction that the acceleration is applied in. The length of the arrow/vector is the distance from tail to head. And for an acceleration vector, it is the amount of acceleration that will be applied.
SI Units
If you're new to physics, you may not be familiar with SI units. SI units are standardized units of measurement known as the International System of Units. One thing that you will learn in physics is that the units of measurement are every bit as important as the numbers when doing math. Physicists around the world have chosen to follow this agreed upon standard of measurements. You will see SI units used pretty much anywhere the physics is discussed.
Force is measures in units called "Newtons" (named after Sir Isaac Newton). A Newton is a
So, an acceleration vector stores the amount of the acceleration which is a "kilogram meter per second each second". You will encounter weird measurement names like this quite often in physics. There is a method to the madness. A Newton is the amount of force necessary to accelerate a kilogram of mass one meter per second every second. So, kilogram is obviously our unit of mass. Meter is our unit of distance. A Velocity is basically a speed and so will be measured in meters per second. So, a Newton is the amount of force required to increase the velocity of a one kilogram object by one meter per second for every second it is applied. Seconds each second is often expressed as seconds squared by the way. So, meters per second squared, just means meters per second each second.
Force
So, I believe it was Sir Isaac Netwon who figured out that a Force is equal to a mass times an acceleration. (F=ma) So, our acceleration is basically a force without a mass. Instead of kilogram meters per second each second. It's just meters per second each second. Without the mass, there is no kilograms.
Acceleration
So, our unit of acceleration is the meter per second (which is a velocity) each second. So, every second you are increasing a velocity by one meter per second. An acceleration is really a change in an object's velocity. Velocity is a change in position over a specific period of time. In SI units a velocity is a change in position of exactly one meter per second. An acceleration changes velocity and so also has to be applied over time, which is where you get meters per second each second. A velocity is measured in meters per second, and the acceleration is a change in velocity (also known as a change in meters per second) applied each second.
We can use algebra to rewrite Newton's formula to say that an Acceleration equals a Force per Mass. (a = F/m) In more plain English, that basically says that an acceleration is the result of applying a specific force to a specific mass and is inversely proportional (in other words, the more mass the less acceleration caused by the same force).
Now we have a formula we can use to determine our accelerations
Applying Acceleration to a Space Ship
One of the easiest ways to start working with acceleration is in space. In space, you don't have things like wind resistance or gravity to complicate things. In space, when you push something it will continue like that forever until another force acts to change it.
Now it may be obvious that when you push an object in space that it will move in that direction. But what may not be quite so obvious is that there are really two possible results from a push. Besides just movement, a push can cause an object to rotate.
Take a look at this drawing:
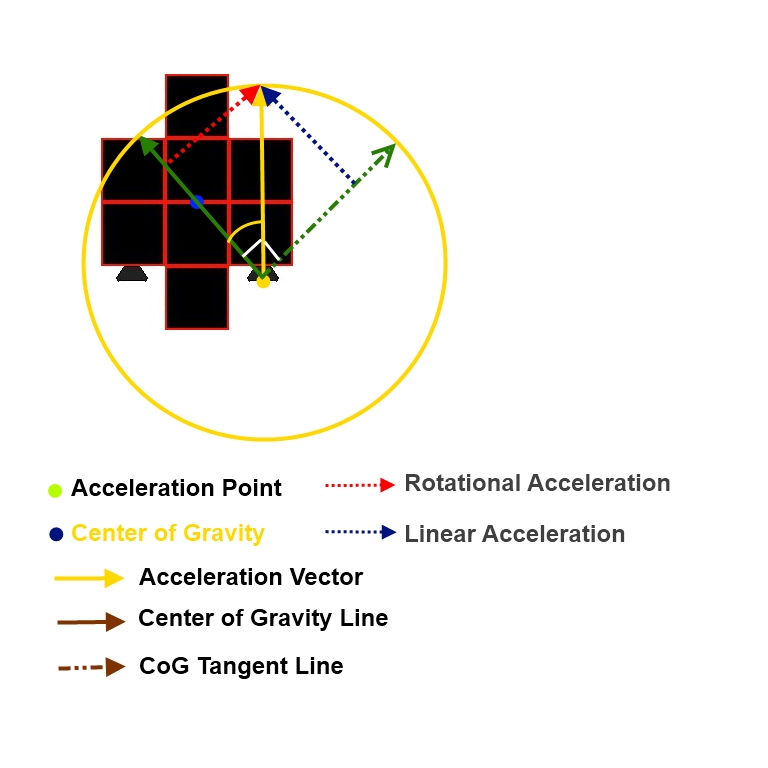
The yellow dot in the drawing represents the spot on our space ship where we push the spaceship. In this case, it represents the position where the starboard engine is attached to the ship. The engine pushes on the ship in the direction of the yellow "Acceleration Vector". The direction of this arrow/vector is the direction that the push, or force, is applied in. The length of the arrow/vector should store is the amount of force applied, or actually in our case we will immediately divide by the mass of the ship to convert it from a force vector to an acceleration vector. So, if you divide the force vector by the ship's mass, the result will be our "Acceleration Vector" here.
Now don't get confused. You may be saying, "I thought vectors always have their tail at the origin of 0,0." They do. Vectors never have position. The yellow "Acceleration Point" dot is a position, not a vector although we will likely store it in a vector object to make the vector math easy. But its not really a vector. And we've visually positioned the "Acceleration Vector" starting at the "Acceleration Point", but vectors never have position; because a vector only represents a direction and an amount, position is never relevant. Regardless of where this acceleration is applied, it is applied in the direction of the arrow and has the amount represented by the length of the arrow.
Rotation vs. Movement
Just from living in the real world, you should know that sometimes when you push on an object it rotates and sometimes it moves and you could get a combination of the two. So, how does this work?
Well, basically, when you push directly towards an object's Center of Mass, or Center of Gravity, the object will move in the direction of the push. In our drawing above, the Center of Mass is represented by the blue "Center of Gravity" dot. You can think of this as the center of the object, but its actually the place where all of the object's mass is balanced out. In a doughnut, the center of gravity is in the space of the hole in the doughnut's center. So, the center of gravity may not even be inside of the object or necessarily located at its center. It's the point where you could suspend the object from and it's mass/weight would balance out in all directions. But for simplicity's sake, you can just think of it as the center of the object.
The green "Center of Gravity" line/vector/arrow is a line between the point on the object where the push/acceleration is applied to the object's center of gravity. When the push is in the direction of this line the object will be accelerated along the line and no change in rotation will occur. All of the energy of the entire push will go to moving the object.
So how do you get an object to rotate? If you push the object in a direction perfectly perpendicular to this line, you will cause the object to rotate instead. So, a push at exactly 90 degrees away from the "Center of Gravity" line will result in a change in the object's rotational velocity, or rate of spin.
Torque
A twisting force like this is known as Torque. A torque is a rotational force that is applied at a given distance from the rotational center. I call this distance the "torque arm". Basically, the force is multiplied by the length of the torque arm, which could increase or decrease the resulting acceleration. So, the further away from the object's center that the torque is applied, the greater the resulting torque will be which is then divided by the object's mass to get the angular acceleration.
Angular Acceleration
The "angular acceleration" is the rotational acceleration that will be applied to the current rotational velocity where rotational velocity is how fast the object is currently spinning.
The dotted green "CoG Tangent Line" is the line that is perpendicular to the Center of Gravity line. If our engine were to push our ship in that direction, the result would be an acceleration in the rotational speed of our ship. The ship would not increase in velocity, but instead all of the energy of the force would go towards changing the ships rate of spin. If the ship were spinning clockwise, then the counter-clockwise acceleration would subtract from the rate of spin instead of add to it, just as an opposite direction linear push would slow the ship down instead of speed it up.
The force applied, when applied perpendicular to the center of gravity line, will add to the rotational speed of the ship by the amount of force times the length of the torque arm divided by the mass of the ship which will be the angular acceleration rate.
The Question
Now maybe we should take a step back and figure out the question that we are trying to solve. Basically, we want to know how the ship will move and/or spin when some force (the ship's engine) pushes on the ship.
The "Acceleration Vector" in the drawing above represents the direction and acceleration amount of the push of the starboard engine. It is not aligned with the "Center of Gravity" line and so we know it will cause some rotation. But its also not aligned with the "CoG Tangent" line either and so we know it will cause the ship to move as well as spin.
We know that movement happens along the "Center of Gravity" line and that rotation happens basically in the circular direction of the "CoG Tangent" line. Both the movement (linear acceleration) and spin (angular acceleration, or rotational acceleration) happen along these two lines.
So, the question can be seen as "What linear acceleration vector combined with what rotational vector will produce an acceleration equal to our original 'Acceleration Vector'?" Or you could also say, "What rotational push combined with what movement push would give us a result of our 'Acceleration Vector'?" Basically, we're breaking the "Acceleration Vector" down into two vectors that combined will equal the "Acceleration Vector". The two vectors we are breaking it down into are the "Linear Acceleration" vector (which will go in the direction of the "Center of Gravity" line) and the "Rotational Acceleration (or Angular Acceleration)" vector (which will go in the direction perpendicular to the "Center of Gravity" line).
That pretty much completes the drawing above. When an acceleration is applied to the ship at the "Acceleration Point", we need to break it up into a "Linear Acceleration" and a "Rotational Acceleration".
Notice that this forms a rectangle with one corner at the "Acceleration Point" and another at the "Center of Gravity" point, making one side of the rectangle along the "Center of Gravity" line and another side of the rectangle along the line perpendicular to the "Center of Gravity" line.
Now both the "Linear Acceleration" and "Rotational Acceleration" are vectors and so their position does not matter. Their direction will be in the same directions as the two sides of the rectangle we have already defined. And because their position is unimportant, we can move them to form the two opposite sides of the rectangle. Their lengths will be the exact answers that we are looking for. (Remember that their directions, again, will be in the direction of the "Center of Gravity" line and perpendicular to that line. So, they meet the definition of a vector by representing a direction and an amount. Their amounts will be the amount of acceleration produced in those two directions. So, their length will be the amount of acceleration produced in those two directions.
Determining Linear Acceleration
Now at this point, this just becomes a trig problem. If you don't know trig, I'll walk you through this. Trigonometry is the mathematics of measuring the universe using triangles, mostly right triangles. And our rectangle here just happens to form a right triangle.
Basically, we are going to start by finding the angle between the "Center of Gravity Line" and the "Acceleration Vector". In code, both of these lines will be vectors although the "Center of Gravity Line" is really a line and not really a vector since we don't really care about it's length/amount. A normalized vector is usually used to represent a direction without an amount because a normalized vector always has its length set to one unit. Once we have the angle between these two lines, we can find our answers.
The "Acceleration Vector" has the length of the hypotenuse of our right triangle (the hypotenuse is the side of a right triangle that is opposite the right angle and is always the longest of the 3 sides.)
We can use SOH - CAH - TOA from trigonometry to find the lengths of the two vectors we are searching for (we already know their directions now we need their amounts).
The Opposite side of the triangle has the exact length of our rotational vector. The Sine of an angle is equal to the ratio of the side Opposite to the Hypotenuse side. So, the side Opposite is equal to the Sine of the Angle divided by the Hypotenuse. So, the amount of rotational acceleration will be equal to the Sine of the Angle divided by the length of the "Acceleration Vector". And voila, you have your rotational acceleration amount.
Determining Angular Acceleration
The Adjacent side (the one touching our angle that is not the hypotenuse or the Opposite side) of the triangle has the exact same length as the side of the rectangle opposite from the Adjacent side. So, finding one will give you the other.
So, the Cosine of the Angle equals the ratio of the side Adjacent over the Hypotenuse side of the right triangle. Or to rework that with a little algebra: The side Adjacent equals the Cosine of the angle divided by the length of the Hypotenuse. Or in a more usable form: The amount of "Linear Acceleration" is equal to the Cosine of the angle divided by the length of the "Acceleration Vector". So, you could take a normalized vector pointing down the "Center of Gravity" line and multiply it times the "Linear Acceleration" amount and produce a vector that represents the linear acceleration. If you add that vector to the velocity vector of the ship, you will get the resulting change to velocity.
Velocity, Linear and Angular
Notice that the ship's velocity is a completely separate vector. The ship's velocity points in the direction that the ship is currently traveling (if the ship is not moving its a zero'ed out vector). It's length is the velocity (or speed) of the ship measured in meters per second. Every second, you can apply our "Linear Acceleration" vector to this ship's velocity vector to change the ship's velocity vector (both direction and amount). You do this by adding the "Linear Acceleration" vector to the Velocity vector.
Basically, what this means is that any time the engine is on it is modifying the ship's velocity. This could be either to speed it up or slow it down, because it's entirely dependent on the direction of the "Linear Acceleration". If the engine is not on, the ship will continue to move at its current velocity both linear and rotational. So, once your object starts to move or rotate, it will continue to do so until something acts to stop it, forever. This is basically the "law of inertia" from physics.
Pushing at an Angle
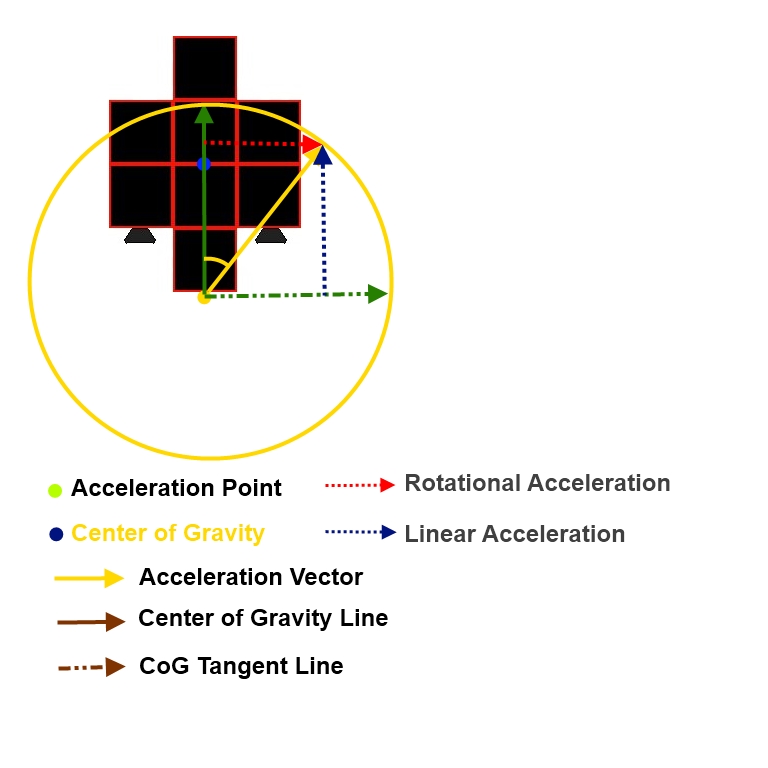
Now in this second drawing, I've moved the "Acceleration Point" to represent a main engine that is centered with the ship. It's "Center of Gravity" line is going to be straight down the ship. But this engine can change it's angle so that it pushes in a variable direction. The push still happens at the "Acceleration Point", but now the direction is variable. In this particular case, the direction is in the direction of the "Acceleration Vector" shown. The math is no different. The only thing that has changed is the "Acceleration Point" and the "Acceleration Vector". Where the other two engines were fixed in one directions and the direction of their acceleration vectors could not change, this engine can change the direction of its "Acceleration Vector". None the less, the calculations remain the same.
One Last Little Bittie Thing (that's huge)
One last thing, don't forget to divide by the number of frames per second. This is real world physics and so it's measured in SI units. But in a game your updates are likely applied every frame which is probably much faster than 1 frame per second. So, all of the times (seconds) have to be converted to frames, which means any time you use a second unit it needs to be divided by frames per second to convert it to frames. For example, all accelerations are applied "per frame" and thus should be in "meters per second each frame" rather than meters per second each second".
May the Force be With You Always
Accelerations are useful for all sorts of things when it comes to vehicle physics, whether its gravity itself or the force of the wind in a boat's sails, every push on the vehicle is an acceleration. So really this is just the beginning of your journey in vehicle physics. None the less, understanding acceleration will get you off to a real good start.
Summary...
This is a discussion of the algorithm for accelerating 2D game objects. It is meant to help understanding before reading the source code provided as a tutorial.